逆三角関数の微分

の微分を求めます。(arcsinxの微分)

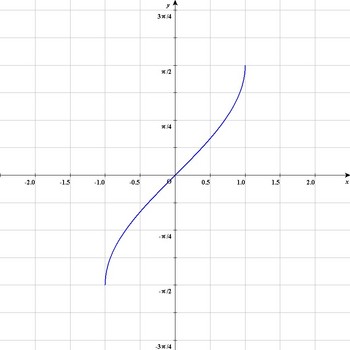
図　y=arcsin x

 

元の関数y=sinxの微分は知っている。 

ですから公式、逆関数の微分

を使います。（証明は教科書等で確認しよう）

 

だから、

 ここでcos yについてわかりやすいよう図形的にみてみましょう。

つまりy=arcsin xにおいてcos yを求めます。

図形はこの通りですね。

yの値域からy≧0に注意して。（グラフを見れば傾きが常に正なのでここからも明らか）

三平方の定理から（もしくは図を使わずにsin^2 θ + cos^2 θ =1から求めてもよい）

ゆえに

以上から、

 

cos^-1(x)も同様に

これより、

なので

定数(constant)をとります。x=0を代入してもとめると、重要性質

が得られます。次はタンジェント。

y=tan^-1(x) とすると、その微分は、

微分はこれですべて終了。

---

今度は逆正弦関数と逆正接関数の関係

式で求めてもいいですが上の図から

---

これで「体積を求める」の解法③の準備が整いました。

 

 

 

タグ：逆三角関数の微分 微分 逆三角関数

逆三角関数

高校ではいろいろな関数を学びました。

指数関数、分数関数などなど。

 

そして数Ⅲでは逆関数を学び、対数関数が指数関数の逆関数であることや

定義域や値域の問題にも触れました。

 

しかし三角関数の逆関数はどうでしょう？

そうです！多項式の関数や指数関数の逆関数は学んだのに

三角関数の逆関数だけ教科書には載っていません。

 

今まで数学の入試問題をたくさん解いてきましたが

逆三角関数で解いたら楽になのになぁ、と

思う問題が少なからずありました。

 積分計算が簡単になったり積分できる関数が

飛躍的に増えるのになんで学校で習わないんだ？

とか今では思います。

 

そんなに難しいことではないです。

僕が自力で逆三角関数を考え微分や積分ができたぐらいです。

 

有理関数の積分が統一的に理解できます。 

 

このように逆三角関数を学ぶメリットは大です。

 

 

さて、逆三角関数の重要性がわかってもらえたところ（？）で

高校数学の知識から三角関数の逆関数に

ついて考えていきたいと思います。

 

三角関数の逆関数を「逆三角関数」といいます。

あらわし方は

と書きます

 

三角関数の意味について復習してみます。 

図形的な三角関数の定義では 

三角関数は角度が与えられたら直角三角形の

二辺の比の値が確定します。

つまり

角度→辺の比

 

それでは逆関数の場合はどうでしょう。

逆関数の定義からわかるように「逆」なのですから

辺の比→角度

になります。

 

これが逆三角関数のイメージです。

ではきちんと数学的に逆三角関数を定義していきますよー。

 

 

下の「続きを読む　～数学的に逆三角関数を定義する～」をクリック！

（無い場合はそのまま下へ）

 

 

続きを読む　～数学的に逆三角関数を定義する～

タグ：逆三角関数 三角関数 逆関数

体積を求める－その４

問題の解答

 

補足の②での解き方を示します。

S(x) は長方形なので面積は（底辺）×（高さ）ですね。

底辺、高さともにx の関数なので前の解答のように

底辺をb(x)、高さをh(x) と置くことにします。

 

 

 図1　底面

 

 図から三平方の定理より

 

図2

図より

よって面積は

よって体積Vは

ここで

と置換すると

ゆえに

積分範囲は

x:0→rより

t:-r^2→0

 

前と同じ結果が得られました。

 

タグ：積分 微分積分 体積

体積を求める－その３

「体積を求める」の解答編です。

 

（1）

これは簡単。円柱の体積の半分ですから

 ですね。

 

（2）

前の補足で示した①に沿った解答を書きます。

図1

まずはじめに三角形の面積つまりS(x)を求めます。

図形は三角形なので（底辺）×（高さ）÷（2）ですね。

図からわかるとおりxが-rからrに変わるまで底辺、高さとも

変化します。ですから底辺、高さをxの関数とみてそれぞれ

b(x)、h(x)

とします。ゆえに面積S(x)は

ですね。つぎに具体的にb(x)、h(x)をxで表してみます。

まずは底辺b(x)から

図1を真上から見ます。

そうすることで求めるb(x)がわかります。

三平方の定理より

 

となります。あとは高さh(x)です。

 

図1を横から見ます。斜めの線は水面です。

さて高さを求めるわけですが、xが-rからrまで動いても

「傾きh/rは変わらない」ということに注目します。

底辺b(x)がわかっているので

となることがわかると思います。

 ここまででb(x)、h(x)が求まったのでS(x)を求めます。

あとは積分。あと少しです。

図　r=1、h=1のとき 

これで体積が求まりました。

お疲れ様でした。

②、③での解答も順次載せる予定です。

タグ：体積 積分 微分

体積を求める－その２

前の問題の補足説明

 

3通りの切り方を示します。

①

 

 

灰色の図形が切った断面。

断面積をS(x)とすると体積Vは

 

折り紙を何百枚も重ねれば直方体になるように（？）

うすーいS(x)を-ｒからｒまで集めて足し合わせれば

求めるVになる、というイメージです。

 

以下同様に

②

 

求める体積Vは

 

③

 求める体積Vは

 

 の3通り。

 

計算量（≒難易度）は　①＜②＜③

 

試験のときは早く解く必要があるので断面積の「形」をみて

①三角形

②長方形

③？

なので①、②が解きやすそうだと判断するのがよさそうです。 

 

 

③は大変ですが「逆関数」の知識があれば高校数学の発想を自然に発展させればできるかな。

 

僕は最初③しか思いつかなかったので計算が大変でした

 

数学記事一覧

 

タグ：微積分 体積 高校数学