逆三角関数 [微積分]
高校ではいろいろな関数を学びました。
指数関数、分数関数などなど。
そして数Ⅲでは逆関数を学び、対数関数が指数関数の逆関数であることや
定義域や値域の問題にも触れました。
しかし三角関数の逆関数はどうでしょう?
そうです!多項式の関数や指数関数の逆関数は学んだのに
三角関数の逆関数だけ教科書には載っていません。
今まで数学の入試問題をたくさん解いてきましたが
逆三角関数で解いたら楽になのになぁ、と
思う問題が少なからずありました。
積分計算が簡単になったり積分できる関数が
飛躍的に増えるのになんで学校で習わないんだ?
とか今では思います。
そんなに難しいことではないです。
僕が自力で逆三角関数を考え微分や積分ができたぐらいです。
有理関数の積分が統一的に理解できます。
このように逆三角関数を学ぶメリットは大です。
さて、逆三角関数の重要性がわかってもらえたところ(?)で
高校数学の知識から三角関数の逆関数に
ついて考えていきたいと思います。
三角関数の逆関数を「逆三角関数」といいます。
あらわし方は
と書きます
三角関数の意味について復習してみます。
図形的な三角関数の定義では
三角関数は角度が与えられたら直角三角形の
二辺の比の値が確定します。
つまり
角度→辺の比
それでは逆関数の場合はどうでしょう。
逆関数の定義からわかるように「逆」なのですから
辺の比→角度
になります。
これが逆三角関数のイメージです。
ではきちんと数学的に逆三角関数を定義していきますよー。
下の「続きを読む ~数学的に逆三角関数を定義する~」をクリック!
(無い場合はそのまま下へ)
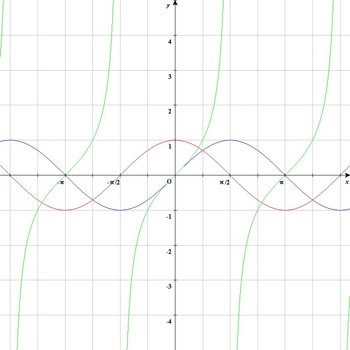
おなじみに三角関数のグラフです。
例えばこの中の
の逆関数を求めてみます。
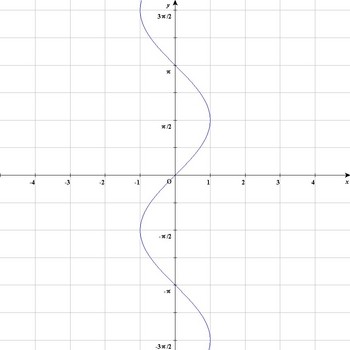
yとxを入れ替えてみます。
グラフを書いてみるとx軸とy軸が入れ替わるのだから
このようなグラフになります。
と書いた関数がsinの逆三角関数で
上のグラフの曲線になるんだなぁと思ったら間違いです。(グラフが違う!)
中学生で学んだ「関数」の意味を思い出してください。
与えられた変数xの値に対して1つの値yが定まるとき、その対応関係を
「関数」と呼ぶのでしたね。
もう一度グラフを見てください。
xが1つ決まるとなんとたくさんの、というか無限個のyが
出てきてしまいます。
これでは「関数」とはいえません。
さて、それではどうするか。
xが1つ決まったらyが1つ決まれば良いのです。
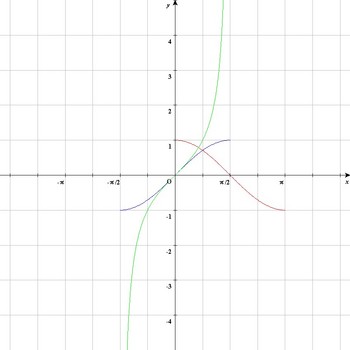
そのようにするためちょっと三角関数の細工します。
このように三角関数の定義域を制限します。
ここでは定義域の制限を強調するため頭文字を
大文字にしました。
制限をかけた三角関数グラフはもちろん下図のようになりますね。
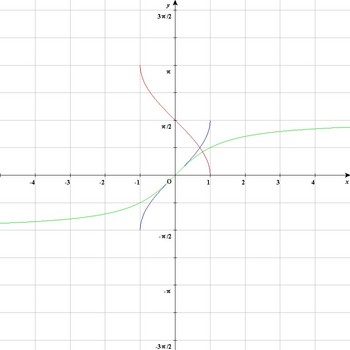
それではxとyを入れ替えたグラフを見てみましょう。
どうでしょう?
ちゃんとxがひとつ決まればyがただ1つ決まるようになりました。
これでしっかり「関数」として逆三角関数が定義できそうです。
制限した三角関数をxについて解いてx,y入れ替えた式を
と書いたのは「逆三角関数」になります。
読み方は上から「インバースサイン」「インバースコサイン」「インバースタンジェント」です。
このように「逆の」を意味する「inverse」を前につけるだけです。
※「arcsin」と前にarc(数学用語で「逆の」を意味する)を書いて
「アークサイン」と読む場合もあります。cos,tanについても同様。
やっと逆三角関数を定義できました!
グラフはもちろん上と同じ。
ひとつ例を挙げましょう。
このように使います。
ここで注意!
当たり前ですね。(他も同様)
ちなみに
と書きます。上から
余割(コセカント:cosecant)
正割(セカント:secant)
余接(コタンジェント:cotangent)
僕は今のところこれらは使える頻度が少ないので使っていません。
なんか6つもあると混乱しそうだし・・・。
ここまでで逆三角関数を定義してきましたが、
これが何の役に立つんだとか思うかもしれませんが、
本当に役に立つのはこれらの関数で微分や積分の計算するときです。
もちろんこの知識だけでも解ける問題が広がりますが。
本当は逆三角関数の微分までやりたかったのですが
予想外に長くなったので次回にします。
これで「体積を求める」の問題に③の方法で解く準備が整います。
それではまた次回。お楽しみに。
~さらに学びたい人へ~
「マチンの公式」で調べれば面白い等式が出てきますよー。
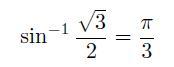
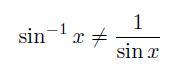
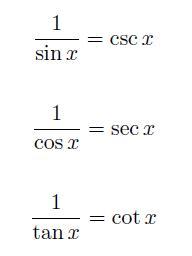




コメント 0