フィボナッチ数列の拡張 「離散」から「連続」へ

フィボナッチ数列、これほど自然界に不思議と調和した数列はないだろう。フィボナッチ数列の話題には事欠かないが今回、この数列を拡張し、連続した関数にすることを試みる。

---

まずはフィボナッチ数列の「定義」から。

Fnを求めるためには1つ前の数と2つ前の数を足せばいいことがわかりますね。

これよりF2=F1+F0=0+1=1

F3=F2+F1=1+1=2

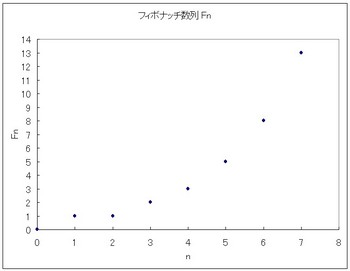
と順次求めていけます。グラフにしてみると、

 図1　Fn (0≦n≦7)のグラフ

n=1,2で1,1と同じ数字が続くところがグラフとしてちょっとしたアクセントがあって（？）面白いところですね。n=7以上は急激に増加していきます。

 

やっぱりグラフは連続でないと面白くないですよね。

これからフィボナッチ数列を拡張していきます。nを自然数から整数へ。整数から実数へ。

1、1と連続する不思議な構造の謎がわかってきます。

 

そこでエクセルで連続したグラフを描くことを目標にします。（複素数の分析ツールを使わずに）

 

自然数から整数への拡張

定義式を変形して見方を変えます。すなわち、

すなわちFnを求めるには正の方向に2つ進んだ数から1つ進んだ数を引けば良い。

F(-1)=F(1)-F(0)=1-0=1

F(-2)=F(0)-F(-1)=0-1=-1

F(-3)=F(-1)-F(-2)=1-(-1)=2

F(-4)=F(-2)-F(-3)=-1-2=-3

…

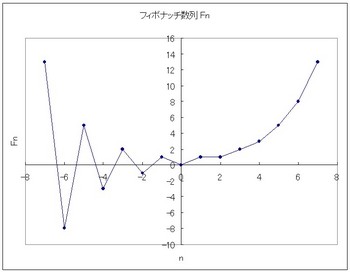
と求めることができる。グラフにすると、

 図2　Fn (-7≦n≦7)のグラフ

変化が見やすいように線で結んでみた。

正負を繰り返しだんだん大きくなる。|F(-n)|=F(n)の関係が成り立つようだ。

詳しく言うと、n=-2k (kは自然数)のときF(-n)=-F(n)。

n=-(2k-1)のときF(-n)=F(n)となるようだ。（証明略）

これから連続したグラフを求めていくけど、このグラフからn=2.5のときF=1.5だと言っているんじゃないよ。念のため。

 

実数へ！ 

 定義式から、この数列の一般項がわかります。導出はここでは行いませんが、高校で習う漸化式の特性方程式を利用する方法の他に、行列を用いる方法、母関数を用いる方法…といろいろ求め方があるので試してください。

フィボナッチ数列の一般項。

不思議ですよね。整数列なのに√5と無理数が出てくるところとか。

実数に拡張するのでnではちょっと違和感があるのでxの関数としてみます。もう数列ではないので「フィボナッチ関数」と名づけます。

さて、今度は実数へ拡張するのでxに2.5とか-0.7とか代入して求めてみよう！ということなりますがここで問題が。

例えば、計算するときに

 この値すぐにわかりますか。エクセルで計算させるとエラーになりますよ。

括弧の中が問題で負の値になっています。そういえば-1を1/2乗すると√(-1)で虚数が出てきます！（-1の2乗根は±iで二つ出てくるなど複素平面を用いてn乗根の話をしたいところですがここではエクセルでフィボナッチ関数のグラフを求めることのみを目指して厳密な理論抜きで突っ走ります。）

ちなみに、上式の値は約0.43+0.74i。

つまり負の値のx乗を求めるにはどうすれば良いか、ということ。

ここで登場するのが「オイラーの公式」。

この公式の導出はここでは略します。詳しく知りたい場合はWikipedia等に証明があるので見てください。見てもさっぱりわからん(。-`ω´-)ﾝｰな人は一番下におすすめのわかりやすい本を紹介しておいたので見てみるといいですよー。

θに円周率πを代入すると

有名な「オイラーの等式」ですね。美しい・・・。

よく見てください。右辺は-1で負の値ですよ。これは利用できる！

両辺をx乗して計算してみます。

xがどんな値だろうと右辺が三角関数なのでエクセルで計算できる！

これを利用して　　（a^x=|a|^x・(-1)^x、ただしaは負）

 

となる。もとの式に代入して、

エクセルで計算させるときiがあると計算できないので複素数の実部と虚部を分けます。

実部をRe(x)、虚部をIm(x)とします。（例えば複素数x=3+4iのときRe(x)=3、Im(x)=4） 

 

となります。これで積分や微分ができるようになり。曲線を解析的に調べることができる。

これから分かることはF(x)はほとんど複素数だってこと。実数のときはsinπx=0、つまりxが整数のときのみ。 

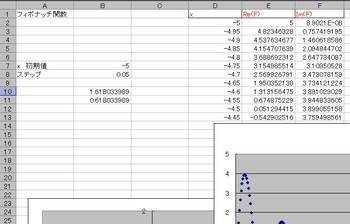
それではエクセルで計算実行！

こんなかんじで計算した。一般項中の黄金比は予め左下で計算しておいた。クリックで拡大できる。

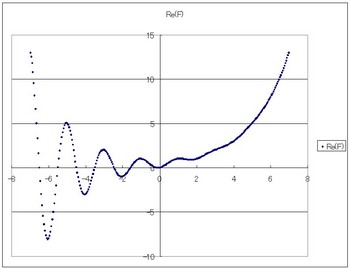
 最初に紹介するのは横軸がx縦軸がRe(F(x))のグラフ。つまりxが変化するとフィボナッチ関数の実数部分はどう変化するのかということ。

図3　Re(F)-x

おお！！ちゃんと図2と合ってます！！1,1も通ってるし、途中の非整数部分もわかります。こんなふうになっていたんですねー＾＾。

xが非整数のときは複素数となるが、このグラフではその複素数を実軸に射影した値をグラフ化しているとわかりますね。

今度は横軸がxで縦軸がIm(F(x))のグラフ。

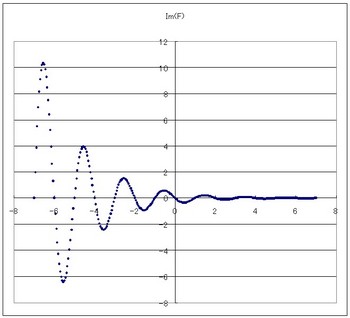
図4　Im(F)-x

減衰する振動曲線ですね。三角関数だから当たり前か！。

縦軸が0になるときIm=0つまり実数となる。

 

 

 複素平面上でのフィボナッチ関数

今度は複素平面上でどのように動くか見てみます。つまり、横軸がRe(F)、縦軸がIm(F)。ここでxは媒介変数となり、グラフ上である点の時xの値が何であるか明示できないことに注意。

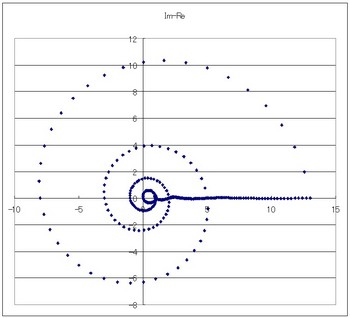
図5　-7≦x≦7　xの間隔0.05

xは反時計回りで回転しています。 

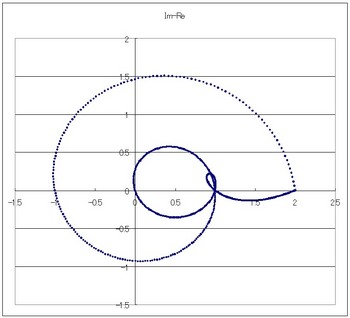
原点付近を拡大。

図6　-3≦x≦3 xの間隔0.01

面白い形です。

x=-3のとき(2,0)ではじまり、180度左回りして(-1,0)。これを繰り返して

(2,0)→(-1,0)→(1,0)→(0,0)→(1,0)→(1,0)→(2,0)

フィボナッチ数列ですね。特に1から1へのくるっと回るところが面白いですね。フィボナッチ数列の裏の構造がわかってきました。

ところで、高校2年のときにフィボナッチ数列を連続的に見たいと思い、数学がものすごく出来る友人と研究（といってもほとんど教えてもらっていたのだが・・・）した。それでこの図6を見て彼は「リンゴの皮みたい」と言って私は何を言い出すんだ？、と一瞬戸惑った。しかし良く見ると確かにそのようで言い得て妙なり！と思った。出来る人は発想が豊か！？

 

三次元空間でのフィボナッチ関数

図3、図4、図5から3Dで見えた人はすごい。xが決まればRe(F)、Im(F)が決まり、複素平面状の一点が決まる。つまりx-Re(F)-Im(F)で曲線を描くことになる。図3、図4、図5はある軸から垂直に真上から見た図ということになる。

三次元のグラフはエクセルでは厳しいので数式処理ソフト「Maxima」についているgnuplotというグラフ処理のアプリケーションを用いることにします。

準備のため、媒介変数tを用いて

 と書き換えてxyz空間上に表示させるようにします。

先程の図3はxy平面、図4はxz平面、図5はyz平面ということになる。

入力は

---

plot3d([t,(((1+sqrt(5))/2)^t-((sqrt(5)-1)/2)^t*cos(%pi*t))/sqrt(5),-(((sqrt(5)-1)/2)^t*sin(%pi*t))/sqrt(5)],[t,-5,5],[y,-5,5],[grid,100,100]);

---

 フリーソフトなのでダウンロードして実際触ってみると面白いよ。おすすめ。

上のコマンドをコピー、そして「shift」+「Enter」でグラフが描かれます。

 

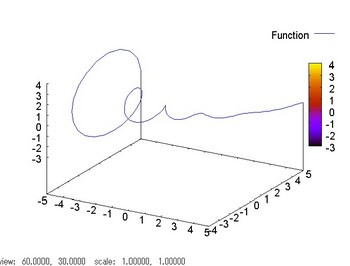
図7　右下に伸びる軸がxで右上方向がy、上方向がz軸

立体的に「リンゴの皮」構造がわかりますね（笑）。

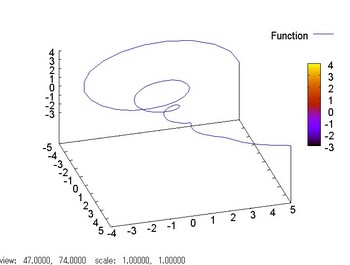
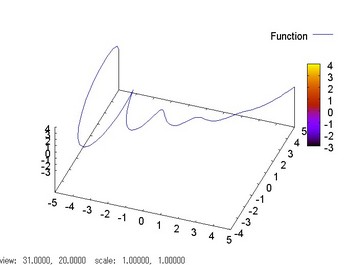
しかし三次元と言ってもそもそも画面は2次元ですから、ちょっと視点を動かさないとわからない。なので少し視点を変えたグラフを見て感じをつかんでください。

 左回りにぐるぐると螺旋を描いていることがわかりますよね。

さて、z=0の平面で切るとその平面上に切られた曲線が点として現れます。この平面は図2と等しいことがわかります。

つまり図2はフィボナッチ数列の裏に隠されたほんの一部の姿でしかないということです。曲線が実数の平面に交わる点が我々が見ることのできるフィボナッチ数列の整数列となる。

ここまで長い記事になってしまいましたが数列の見方がちょっと変わったんじゃないでしょうか。

最後に意欲ある中学生、高校生のために名著を紹介します。もちろん数学が好きな人にも。

オイラーの贈物―人類の至宝eiπ=-1を学ぶ (ちくま学芸文庫)

• 作者: 吉田 武
• 出版社/メーカー: 筑摩書房
• 発売日: 2001/11
• メディア: 文庫

「オイラーの公式」の導き方、付録でフィボナッチ数列を行列で求める方法が書かれています。数学の「美」が味わえる本当に良い本です。数学が体系的にわかります。私は本がぼろぼろで表紙の文字が見えなくなるまで何百回も読みました！

今年新装版として単行本の大きいのが出たようなのでこちらも紹介。

オイラーの贈物―人類の至宝eiπ=-1を学ぶ

• 作者: 吉田 武
• 出版社/メーカー: 東海大学出版会
• 発売日: 2010/01
• メディア: 単行本

 

～参考リンク～

数学って面白い！？　「フィボナッチ数列」

ミルカさんとフィボナッチ数列

 

良かったらクリックお願いします。↓

にほんブログ村

 

この記事（「フィボナッチ数列の拡張　「離散」から「連続」へ」）がINRI1225さんのブログで紹介されました。↓

大自然の摂理　★★★　心と魂の原点復帰　★★★★

 

タグ：エクセル フィボナッチ関数 フィボナッチ数列 Maxima オイラーの公式 複素平面 Gnuplot

コメント 3

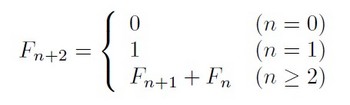
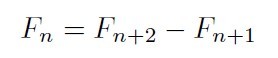
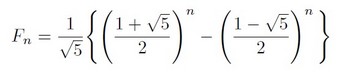
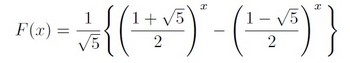
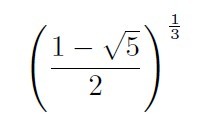
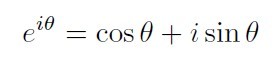
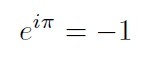
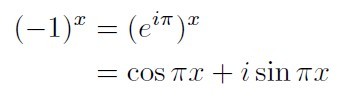
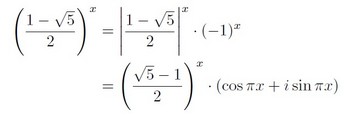
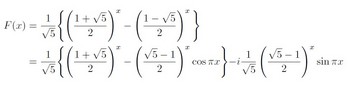
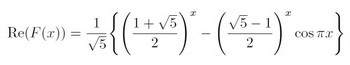
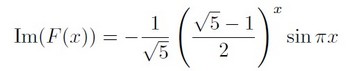
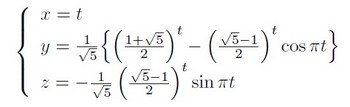
前略　始めてご連絡いたします。勝手に、図表を引用添付させて頂きました。この件で連絡いたした次第です。
　フィボナッチ数列は昔から興味があり、趣味の競馬に援用していましたが、もう少し勉強したくて、このミノー+さんのブログに辿り着きました。私60歳を超える老人でして、どこまで理解できるか解りませんがフィボナッチ数列の素晴らしさだけは、表面的には理解しているつもりです。でも、多分、もっと奥深いところにとても面白いことがあるのではないかと考えています。競馬に援用するなら、引用は困るというのであれば直ぐに削除しますのでご連絡下さい。
e-mail : [e-mail] がアドレスです。
by fineteqint (2011-08-24 04:26) 

フィボナッチ数列を≪拡張し、連続した関数にすることを試みる。≫このことを［黄金長方形］の特性と絡めて［自然数］の［順序数］（離散数）と［量の数］（連続数）の［両義性］を獲得し・されているのを［西洋数学の成果］で≪「離散」から［連続］へ≫について観てみよう。　
　［西洋数学の成果］として、【超越数（［ｅ］）と円周率（π）と無限（∞）と虚数（ｉ『動的作用を持つ』）と［数学的思考］（身体化された心）としての【１　０】の6つのシェーマ（符号）を受け入れて、【［桁表示］の［０　１　２　３　４　５　６　７　８　９］による十進法】の言葉（言語）が生まれ・生まれている【数そのモノ】の［両義性］を観てみる。
　フィボナッチ数列が［有理数］から［実数］やケプラーの見出したどこまで行っても（任意）の項の平方が、その両隣の項の積と［１］だけ異なることを［黄金長方形］の中に次々と縮小（縮約・縮退）していく［正方形］の無限（∞）から掴んだ［単位正方形］であり・あるとすると二次元［直角座標］の［原点］（０）に双対しているとパースペクティブでき・出来ていると観る。
　ここに【数そのモノ】の［両義性］と［実数］を掴み・掴まされている。
　もう一方［黄金長方形］は、［線分］（仮設の1）の全体と部分の比と部分と部分の比から出てきたものを［ｉ］（『動的作用を持つ』）90°（π/２）で組み立てたものと観る。
　この関係を［直角座標］の［原点］（０）から横軸上に［仮設の1］をとり，『自然比矩形』を浮かべる（置く）と［自然数］（離散数）の［１］が［連続数］（実数）の［１］として［ｉ］（『動的作用を持つ』）を介して［ｅ－１］に双対してパースペクティブし・されていると観得る。
　これは『離散的有理数の組み合わせによる多変数創発関数論　命題Ⅱ』の帰結としてパースペクティブでき、［西洋数学の成果である超越数（［ｅ］）と円周率（π）と無限（∞）と虚数（ｉ『動的作用を持つ』）］を容認し・すれば、［カオス］表情を帯同する『縮約（縮退）自然数』として【［桁表示］の［０　１　２　３　４　５　６　７　８　９］による十進法】の［自然数］を掴み・掴まされていると観てよいのではないだろうか。

by 縮約（縮退）自然数 (2019-02-10 05:49) 

　≪…離散的有理数の組み合わせによる多変数創発関数…≫の
［眺望］は、［絵本］「もろはのつるぎ」で・・・　

by 絵本のまち有田川 (2020-01-10 04:52)