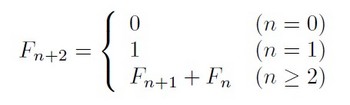トポロジーの発想力 [数学小話]
トポロジー、位相幾何とは、ゴム膜の幾何学。つまりやわらかい幾何学である。と一般向けの位相やトポロジーの本を数冊しか読んでいない受験生がえらそうに言う(笑。だから実際詳しくは知りません。。。
今まで、受験数学関連の数学記事を書こうかと思っていたけど最近受験とは関係なさそうな記事が多い。というのも他にサイトにもっと分かり易い解説等があるからだ。じゃあ、僕がわかる範囲で受験生や一般向けに数学の面白さや自由性が分かってもらえるような記事を書こう!というわけ。
さて、今回はトポロジー、といっても数式は一切使わない。お風呂に入ってて思いついた問題(笑)。(僕が描いた絵は立体感が乏しいですがなんとか想像で補ってください)。
上の①、⑦の図形ですが立体的でゴムの膜で出来ていると考えてください。ただしこのゴムは非常に高性能?で、どの部分をとってもいくらでも伸ばしたり縮めたりすることが出来るとしましす。そして切断不可、面同士が突き抜けたりはしません。
①と⑦は、穴が二つある曲面(ゴム膜)。
さて①と⑦は一見違う図形のように見えます。つまり私たちの普通の感覚では①から⑦、その逆⑦から①にも変形できないように思われます。それでトポロジー的発想をするとどのようなことがいえるのか。
さて問題、「①と⑦の図形は同じ曲面か?
つまり変形してもう一方に変えることが出来るか?」
ちょっとしたクイズです。頭の中でいろいろ変形してみましょう。普通の方法では無理なんだから・・・。
答えは↓
di(n,j,k)のグラフ [数学小話]
「桁」の数学でd関数なるものを定義した。定義しただけなのでつまらなかったと思う。面白くなるのはここからである。面白くなるというのはここでは証明の美しさなどではなく数の振る舞いである。
ここではd関数($d^{j}_{k}(n)$)はdi(n,j,k)と表記します。
外部関数定義で紹介したプログラムを用いてグラフにします。
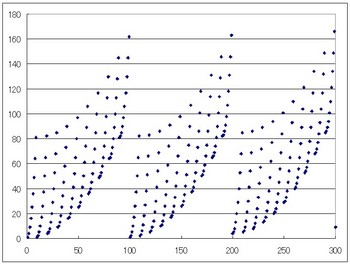
di(n,1,j)のグラフ
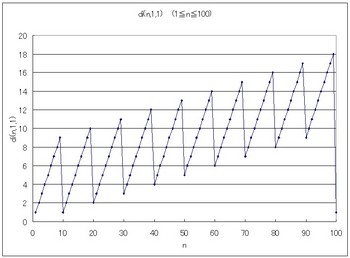
まずは一番簡単なdi(n,1,1)から説明します。di(n,1,1)はある数nの各桁の和を求めるという作業を一回行うという意味でした。たとえば、
di(12,1,1)=1+2=3
グラフを見てみましょう。ある数nを横軸にとり、その数をd関数に入れた値が縦軸にプロットします。
図1 di(n,1,1) 1≦n≦100
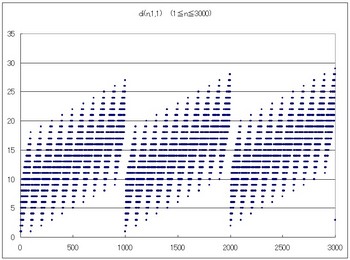
なるほどぎざぎざになる。ちょっと考えれば当たり前ですね。これくらいなら想像できる。下のグラフをnの範囲を広げたもの。
今度はdi(n,1,2)を見てみましょう。これはnの各桁の和を求めるという作業を2回行う。すなわち
di(n,1,2)=di(di(n,1,1),1,1)
と入れ子構造の関数。たとえば、n=39について
di(39,1,1)=12 なので di(39,1,2)=3
となります。
ではグラフを
ひとつだけ飛び出しているのは2999です。
2999→29→11
ここまでは単純明快なグラフでしたがここから複雑で面白くなります。
di(n,2,j)のグラフ
各桁の2乗の和を求めます。例えば、
di(26,2,1)=2^2+6^2=40
ですね。
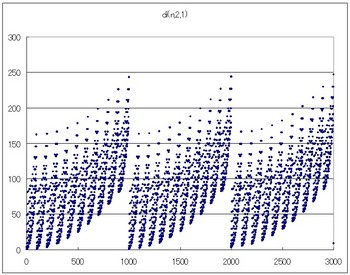
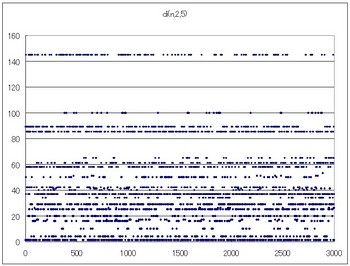
nが1から3000までのdi(n,2,1)のグラフを見てみましょう。
nが1から300までだと
周期的でパターンがあります。
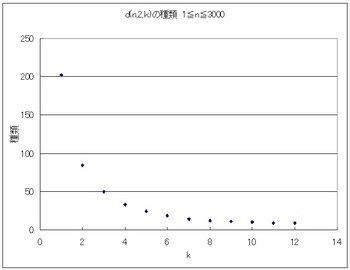
nが1から3000まででdi(n,2,1)の数値の種類は202あります。すなわち最初3000個あった数字がd関数によって202個まで減少するのです。
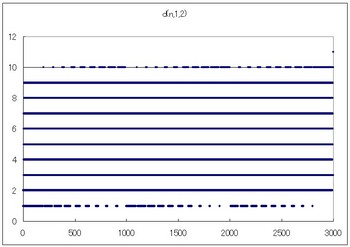
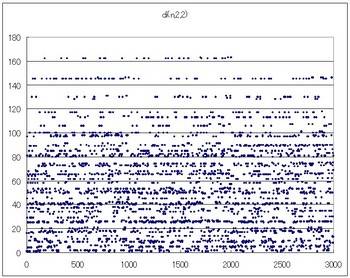
ではdi(n,2,2)のグラフです。
完全にばらばらになりました。しかしよく見ると横に線みたいなものが見える。これを続けるとどうなるのか。面白そうだ。
202が84種類まで減少します。数字の種類が変化しなくなるまで見て見ましょう。
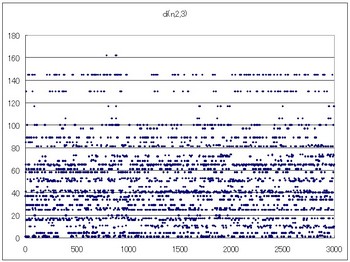
di(n,2,3)のグラフ
84→50まで減。
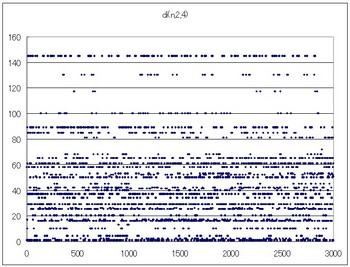
di(n,2,4)のグラフ
50→33
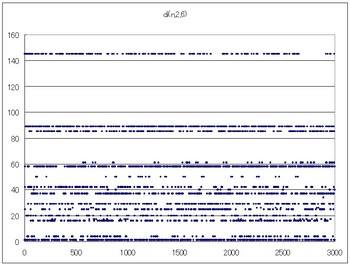
di(n,2,5)のグラフ
33→24
di(n,2,6)のグラフ
24→18
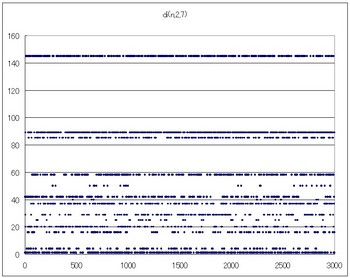
di(n,2,7)のグラフ
18→14
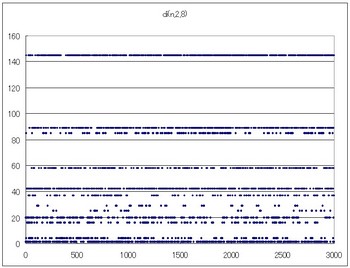
di(n,2,8)のグラフ
14→12
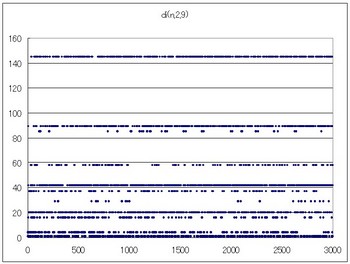
di(n,2,9)のグラフ
12→11
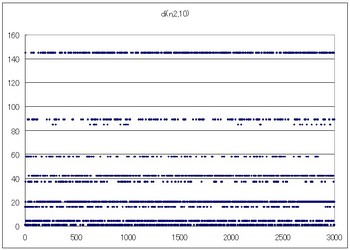
di(n,2,10)のグラフ
11→10
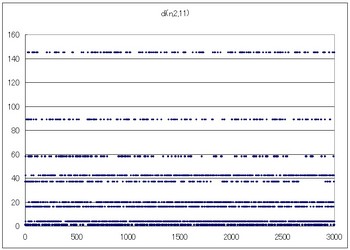
di(n,2,11)のグラフ
10→9
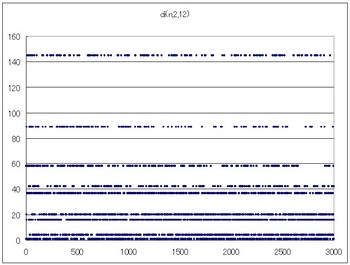
di(n,2,12)のグラフ
9→9
9種類で落ち着きました。これで十分か調べます。ここまで残った数は、
1 4 16 20 37 42 58 89 145
ひとつひとつ調べよう。
1→1→1→…
これは当たり前だ。
4→16→37→58→89→145→42→20→LOOP
なるほど、ループするのか。面白い。
これで9種類でたのでこれ以上減ることは無い。すなわち、これ以上調べる必要はありません。
次にd関数で生み出される種類の変化を見てみる。
なんとなく滑らかに減少することがわかる。
もちろんこれはnの1から3000という数字に依存する。
さて、ここまで見てきたことをまとめると、
自然数nは、「各桁の2乗の和」を求める操作を繰り返すことで「1」と一定になるもの、「4→16→37→58→89→145→42→20→LOOP」となるものの2種類しかない。
と予想できる。
「予想」と言ったのはもちろんnが1から3000までの有限の値までしか調べていないからだ。もしかすると3000より大きい数でLOOPするということが考えられるからだ。完全に上に書いたことが成り立つと言い切るには証明しなければならない。
面白そうだという人は証明にチャレンジしてください。
続く
「桁」の数学 [数学小話]
一年ぐらい前に面白そうだな思っていたものをしっかり定義してLaTeXで書いてpdfにしてみた。クリックすれば大きい画像が見れると思います。
ブログからpdf等のファイルをダウンロードできるような機能があれば良いのになぁ。
「桁」の数学
2を2乗すると4、4を2乗すると16、16の各桁の2乗の和は1^2+6^2=37、37の各桁の2乗の和は58・・・
2→4→16→37→58→89→145→42→20→・・・
これはn乗に一般化したら面白そうだというのがidea。
(仮称)十進BASICについてはこちらからどうぞ
http://hp.vector.co.jp/authors/VA008683/
ソースコード1を下に示す。コピーしていろいろと実験してみる面白い。
INPUT n,j,k
FOR l=1 TO k
LET i=0
FOR d=1 TO 1000
LET i=i+((MOD(n,10^d)-MOD(n,10^(d-1)))/10^(d-1))^j
NEXT d
PRINT l,i
LET n=i
NEXT l
END
ソースコード2
INPUT n,j,k
FOR l=1 TO k
LET i=0
FOR d=1 TO 1000
LET i=i+(INT(n/10^(d-1))-10*INT(n/10^d))^j
NEXT d
PRINT l,i
LET n=i
NEXT l
END
153=1^3+5^3+3^3
まさか、バッハの本を読んでいてこの珍しい数字に出くわすとは思いもしませんでした!
この数列はいろいろと他に面白い性質を持っているのでまた記事を書くと思います。
フィボナッチ数列の拡張 「離散」から「連続」へ [数学小話]
フィボナッチ数列、これほど自然界に不思議と調和した数列はないだろう。フィボナッチ数列の話題には事欠かないが今回、この数列を拡張し、連続した関数にすることを試みる。
まずはフィボナッチ数列の「定義」から。
Fnを求めるためには1つ前の数と2つ前の数を足せばいいことがわかりますね。
これよりF2=F1+F0=0+1=1
F3=F2+F1=1+1=2
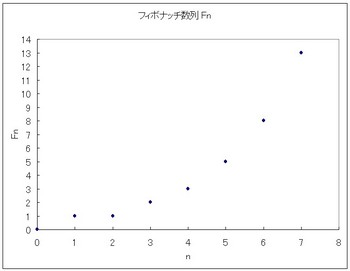
と順次求めていけます。グラフにしてみると、
図1 Fn (0≦n≦7)のグラフ
n=1,2で1,1と同じ数字が続くところがグラフとしてちょっとしたアクセントがあって(?)面白いところですね。n=7以上は急激に増加していきます。
やっぱりグラフは連続でないと面白くないですよね。
これからフィボナッチ数列を拡張していきます。nを自然数から整数へ。整数から実数へ。
1、1と連続する不思議な構造の謎がわかってきます。
そこでエクセルで連続したグラフを描くことを目標にします。(複素数の分析ツールを使わずに)